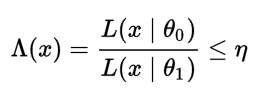Solved Suppose that X1,?,Xn form a random sample from the | Chegg.com
SOLVED: 4. Consider a random sample X1;- X2, Xn from discrete distri- bution with probability function f(rle) 0(1 0)F Iqo12-(c) Find the uniformly most powerful (UMP) test for testing the hypothesis Ho
Solved Let X1, X2,. . . ,X10 denote a random sample of size | Chegg.com
hypothesis testing - Uniformly Most Powerful Test Gamma Distribution - Cross Validated
Lecture 15 — November 12 15.1 Beyond UMP Testing
Illustration of a 1-sided UMP Test in the Normal Setting - YouTube
probability - Uniform most powerful Test for one-sided hypothesis - Cross Validated
hypothesis testing - Confusion regarding plot of p-value as function of MLE value - Cross Validated
Hypothesis Testing in Uniform III V2 - YouTube
SOLVED: Let X1, Xn be a random sample from the Pareto distribution with pdf @x-(0+1) , f(z/e) 0. x < 1. where 0 > 0 is unknown Find a uniformly most powerful (
SOLVED: Let Xn,Xz. Tn be random sample from uniform (0. 0). 0 > 0. In our lecture notes We showed that this uniform family distribution has MLR in X() Accordingly We have
Untitled
hypothesis testing - Uniformly most powerful test in poisson - Cross Validated
hypothesis testing - Uniformly most powerful test in poisson - Cross Validated
Neyman Pearson Lemma - YouTube
Uniformly Most Powerful (UMP) Test: Definition - Statistics How To
Hypothesis Testing in Uniform I V2 - YouTube
The Neymann-Pearson Lemma Suppose that the data x 1, …, x n has joint density function f(x 1, …, x n ; ) where is either 1 or 2. Let g(x 1, …, - ppt download
Solved 1. Let X1,X2,…,Xn be a random sample from the uniform | Chegg.com
PDF) Uniformly most powerful tests for two-sided hypotheses
Monotone likelihood ratio - Wikipedia
Distributed detection and Uniformly Most Powerful tests | Semantic Scholar
Uniformly most powerful test - Wikipedia
Let Xi, , xn be 1.1.d. from the uniform distribution | Chegg.com
hypothesis testing - Using NP lemma to find the most powerful test for uniform distribution - Mathematics Stack Exchange
hypothesis testing - how to get the critical region for a uniformly most powerful test for mean of normal? - Cross Validated
STAT 5520 Unit #6: Uniformly most powerful tests - YouTube
